A simple practice guide for dose conversion between animals and human
- *Corresponding Author:
This is an open access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as the author is credited and the new creations are licensed under the identical terms.
Abstract
Understanding the concept of extrapolation of dose between species is important for pharmaceutical researchers when initiating new animal or human experiments. Interspecies allometric scaling for dose conversion from animal to human studies is one of the most controversial areas in clinical pharmacology. Allometric approach considers the differences in body surface area, which is associated with animal weight while extrapolating the doses of therapeutic agents among the species. This review provides basic information about translation of doses between species and estimation of starting dose for clinical trials using allometric scaling. The method of calculation of injection volume for parenteral formulation based on human equivalent dose is also briefed
Keywords
Calculation, clinical trials, experiment, extrapolation, parenteral, species, starting dose, translation
Introduction
Safe and effective drug dosing is necessary, regardless of its purpose of administration. There are several instances, wherein the initial dose of a particular drug is unavailable in a specific species. Therefore, choosing starting dose of such drugs for research, experiments, or clinical trials in animals and humans is a concern. It should be emphasized that the common perception of scaling of dose based on the body weight (mg/kg) alone is not the right approach. This is primarily because the biochemical, functional systems in species vary which in turn alter pharmacokinetics. Therefore, extrapolation of dose from animals to humans needs consideration of body surface area, pharmacokinetics, and physiological time to increase clinical trial safety. There are four different methods namely dose by factor, similar drug, pharmacokinetically guided, and comparative approaches are described in literature to assess the initial dose. [1] The dose by factor method is an empirical approach and use the no observed adverse effect levels (NOAEL) of drug from preclinical toxicological studies to estimate human equivalent dose (HED). [2] Here, the dose selection is based on minimum risk of toxicity, instead of choosing one with minimum pharmacologic activity in humans. In similar drug approach, the existing pharmacokinetics data for another drug of the same pharmacological category may be used. [3] On the other hand, pharmacokinetically guided approach utilizes the drug activity instead of scaling of dose among species. [4] In case of comparative approach, different methods are utilized to determine initial dose, and the data are compared and optimize to get an initial dose.
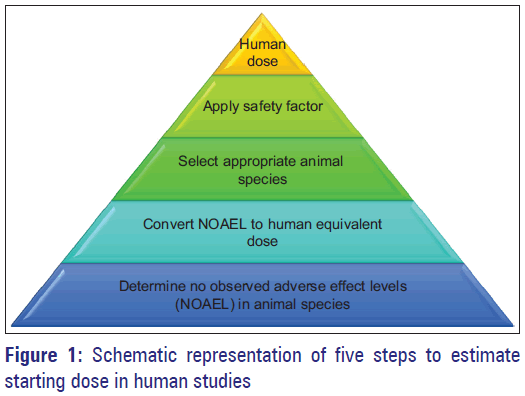
Allometric scaling is an empirical approach where the exchange of drug dose is based on normalization of dose to body surface area. This approach assumes that there are some unique characteristics on anatomical, physiological, and biochemical process among species, and the possible difference in pharmacokinetics/physiological time is accounted by allometric scaling. [5,6] This method is frequently used in research for experimental purpose to predict an approximate dose on the basis of data existing in other species. Drugs with lesser hepatic metabolism, low volume of distribution, and excreted by renal route are ideal candidates for scaling of dose by this approach. The US Food and Drug Administration’s current guidance is based on dose by factor approach where the NOAEL of drug is scaled by making use of allometry to derive the maximum recommended starting dose (MRSD) for clinical studies. [7] This simple empirical approach considers the sizes of individual species based on body surface area which is related to metabolic rate of an animal that is established through evolutionary adaptation of animals to their size. [8,9] Moreover, the MRSD is usually scaled well across animal species when normalized to body surface area (mg/m2). Typically, MRSD is calculated from preclinical toxicology studies and applying a factor. [10] Figure 1 depicts the five steps to calculate MRSD in entry into human studies. Briefly, determine NOAEL’s in animal species, then convert NOAEL to HED, select appropriate animal species, apply safety factor, and finally, convert to pharmacologically active dose. NOAEL, the highest dose level that does not cause significant adverse effects, is a typical index for safety obtained from proper animal experiments to determine a safe starting dose. [7] In step 2, the NOAELs value is converted to HED on the basis of the body surface area correction factor (i.e., W0.67, which depends on the animal weight), using appropriate scaling factors from animal species. [11] Table 1 summarizes the factors for converting doses. The next step is selection of most appropriate species to use in calculation of MRSD. In general, animal species with the lowest HED is considered most sensitive species for determining human risk and is usually selected. [12] However, one can be more accurate by considering the change in pharmacokinetic parameters of drug between species. On the other hand, a specific animal that is more sensitive toward adverse effect can also be a suitable species. In step 4, the HED is divided by a factor value of 10, to increase safety of first human dose. This safety factor is accountable for differences in physiological and biological processes between human and animal species. In the final step, the value obtained is converted to pharmacologically active dose in humans.
| Species | Reference bodyweight (kg) | Working weight range (kg) | Body surface area (m2) | To convert dose in mg/kg to dose inmg/m2, multiply by Km | To convert animal dose in mg/kg to HED in mg/kg, either Divide animal dose by Multiply animal dose by | |
|---|---|---|---|---|---|---|
| Human | 60 | - | 1.62 | 37 | - | - |
| Mouse | 0.02 | 0.011-0.034 | 0.007 | 3 | 12.3 | 0.081 |
| Hamster | 0.08 | 0.047-0.157 | 0.016 | 5 | 7.4 | 0.135 |
| Rat | 0.15 | 0.08-0.27 | 0.025 | 6 | 6.2 | 0.162 |
| Ferret | 0.30 | 0.16-0.54 | 0.043 | 7 | 5.3 | 0.189 |
| Guinea pig | 0.40 | 0.208-0.700 | 0.05 | 8 | 4.6 | 0.216 |
| Rabbit | 1.8 | 0.90-3.0 | 0.15 | 12 | 3.1 | 0.324 |
| Dog | 10 | 5-17 | 0.50 | 20 | 1.8 | 0.541 |
| Monkeys (rhesus) | 3 | 1.4-4.9 | 0.25 | 12 | 3.1 | 0.324 |
| Marmoset | 0.35 | 0.14-0.72 | 0.06 | 6 | 6.2 | 0.162 |
| Squirrel monkey | 0.60 | 0.29-0.97 | 0.09 | 7 | 5.3 | 0.189 |
| Baboon | 12 | 7-23 | 0.60 | 20 | 1.8 | 0.541 |
| Micro pig | 20 | 10-33 | 0.74 | 27 | 1.4 | 0.730 |
| Mini pig | 40 | 25-64 | 1.14 | 35 | 1.1 | 0.946 |
*Data obtained from FDA draft guidelines.[7] FDA: Food and Drug Administration, HED: Human equivalent dose
Table 1: Human equivalent dose calculation based on body surface area*
Key Points in Scaling of Dose
• Larger animals have lower metabolic rates
• Physiological process of larger animals is slower
• Larger animals required smaller drug dose on weight basis
• Allometry accounts the difference in physiological time among species
• Do not apply allometric scaling to convert adult doses to kids.
Dose Calculations and Examples
The dose by factor method applies an exponent for body surface area (0.67), which account for difference in metabolic rate, to convert doses between animals and humans. Thus, HED is determined by the equation:
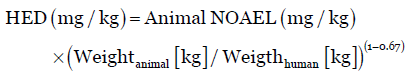 Eq. (1)
Eq. (1)
For example, for a newly developed drug molecule, the NOAEL value in rat weighing approximately 150 g is 18 mg/kg. To calculate the starting dose for human studies, use Equation 1.
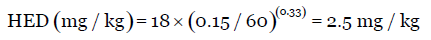
Thus, for a 60 kg human, the dose is 150 mg. This HED value is further divided by a factor value of 10; thus, the initial dose in entry into man studies is 15 mg.
Dose is equally related to body weight although it is not the lone factor which influences the scaling for dose calculation. The correction factor (Km) is estimated by dividing the average body weight (kg) of species to its body surface area (m2). For example, the average human body weight is 60 kg, and the body surface area is 1.62 m2. Therefore, the Km factor for human is calculated by dividing 60 by 1.62, which is 37 [Table 1]. The Km factor values of various animal species [Table 1] is used to estimate the HED as:
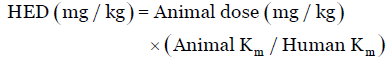 Eq. (2)
Eq. (2)
As the Km factor for each species is constant, the Km ratio is used to simplify calculations. Hence, Equation 2 is modified as:
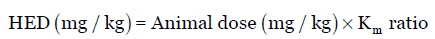 Eq. (3)
Eq. (3)
The Km ratio values provided in Table 1 is easily obtained by dividing human Km factor by animal Km factor or vice versa. For instance, the Km ratio values for rat is 6.2 and 0.162, obtained by dividing 37 (human Km factor) by 6 (animal Km factor) and vice versa, respectively. Thus, usually to obtain the HED values (mg/kg), one can either divide or multiply the animal dose (mg/kg) by the Km ratio provided in Table 1. For example, for a particular drug, the NOAEL in rats is 50 mg/kg. Using Equation 3, HED is calculated either by multiplying or dividing the animal dose with the Km ratio values given in Table 1. Accordingly, divide the rat dose (50 mg/kg) by 6.2 or multiply by 0.162, the HED is 8.1 mg/kg.
However, it must be borne in mind that the km factor varies across animal species and increases proportional to W2/3 within a species as body weight increases. For example, the km value in rats varies from 5.2 (100 g rat), 6 (150 g rat), and 7 (250 g rat). Therefore, calculation of HED for a drug of NOAEL in rats is 50 mg/kg with an average weight of 250 g is as below:
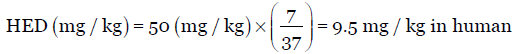
Using the standard km factor value of 6 for rats with average weight of 150 g [Table 1], the dose varies accordingly as seen below:
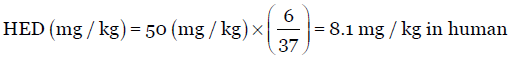
Interchange of unit (mg/kg to mg/m2) of dose of animals or human is carried out using the Km factor [Table 1] as:
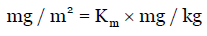 Eq. (4)
Eq. (4)
However, conversion between species based on mg/m2 is not supported for drugs administered by topical, nasal, subcutaneous, or intramuscular routes as well as proteins administered parenterally with molecular weight >100,000 Daltons.
Similar to the HED estimation, the animal equivalent dose (AED) can also be calculated on the basis of body surface area by either dividing or multiplying the human dose (mg/kg) by the Km ratio provided in Table 2. AED is calculated by minor modification of Equation 3 as:
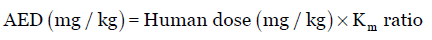 Eq. (5)
Eq. (5)
| Species | Reference body weight(kg) | To convert dosein mg/kg to dose in mg/m2, divide by Km | To convert human dose in mg/kg toAED in mg/kg, either | |
|---|---|---|---|---|
| Multiply human dose by | Divide human dose by | |||
| Human | 60 | 37 | ||
| Mouse | 0.02 | 3 | 12.3 | 0.081 |
| Hamster | 0.08 | 5 | 7.4 | 0.135 |
| Rat | 0.15 | 6 | 6.2 | 0.162 |
| Ferret | 0.30 | 7 | 5.3 | 0.189 |
| Guinea pig | 0.40 | 8 | 4.6 | 0.216 |
| Rabbit | 1.8 | 12 | 3.1 | 0.324 |
| Dog | 10 | 20 | 1.8 | 0.541 |
| Monkeys (rhesus) | 3 | 12 | 3.1 | 0.324 |
| Marmoset | 0.35 | 6 | 6.2 | 0.162 |
| Squirrel monkey | 0.60 | 7 | 5.3 | 0.189 |
| Baboon | 12 | 20 | 1.8 | 0.541 |
| Micro pig | 12 | 27 | 1.4 | 0.730 |
| Mini pig | 40 | 35 | 1.1 | 0.946 |
*Data adapted and modified from FDA draft guidelines.[7] FDA: Food and Drug Administration, AED: Animal equivalent dose
Table 2: Animal equivalent dose calculation based on body surface area*
For example, if the maximum dose of a particular drug in human is 10 mg/kg, the AED is calculated by multiplying the HED by 6.2 or dividing by 0.162; AED is 62 mg/kg.
For parenteral administration, HED conversion (mg/kg) is also based on body surface area normalization. The conversion can be made by dividing the NOAEL in appropriate species by the conversion factor. Guidelines for maximum injection volumes, by species, site location, and gauge size are summarized in Table 3. Injection volume of parenteral formulation is calculated by following equation.
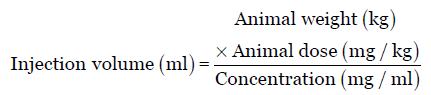
| Species | Route | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subcutaneous | Intramuscular | Intraperitoneal | Intravenous | Intradermal | |||||||||||||||
| Maximum injection volume-ml | Site | Gauge size | Maximum injection volume-ml | Site | Gauge size | Maximum injection volume-ml | Site | Gauge size | Maximum injection volume-ml | Site | Gauge size | Maximum injection volume-ml | Site | Gauge size | |||||
| Human | <2 | Upper arm, abdomen, thigh, buttock | 25-31 | 2-5 | Deltoid, vastus lateralis | 21-23 | 2-5 | Peritoneum | - | <250 | Vein | 18-20 | <0.10 | Dermis | 25-26 | ||||
| Mouse | 1-2 | Back (scruff)/lower abdomen | <20 | <0.1 | Quadriceps, posterior thigh | 25 | 2-3 | Lateral tail vein | 25 | <0.2 | Lateral tail vein | 25 | <0.05 | Lateral abdomen | - | ||||
| Hamster | 3-4 | Dorsum between scapula | <20 | <0.1 | Lind limb, caudal thigh | 25 | 2-3 | Lower left quadrant | 25-26 | <0.2 | Lateral tarsal vein, cephalic/ lingual vein | 26 | <0.05 | - | - | ||||
| Rat | 5-10 | Back (scruff)/lower abdomen | <20 | <0.3 | Quadriceps, hamstring | 25-26 | 5-10 | Lower left quadrant | 24 | <0.5 | Lateral tail/ saphenous vein | 24-27 | <0.05 | Lateral abdomen | - | ||||
| Dog | 100-200 | Dorsum between scapula | 22 | 2-5 | Hind limb, caudal thigh | 22-25 | 100-200 | Cephalic, saphenous | 22-25 | <100 | Cephalic/ saphenous vein | 21 | - | - | - | ||||
| Guinea | 5-10 | Dorsum between | 25 | 0.3 | Lind limb, caudal thigh, | 25 | 10-15 | Lower left | 25 | 10-15 | Lateral | 26-27 | - | Dorsum | 25 | ||||
| Pig | scapula | lumbar muscles | quadrant | saphenous vein | along flank | ||||||||||||||
| Rabbit | 10-50 | Dorsum | 22-25 | <0.5 | Hind limb, caudal thigh | 22-25 | 50-100 | Lower left quadrant | 22 | <5 | Marginal ear vein | 25 | <0.10 | Dorsum along flank | 25 | ||||
| Monkey (rhesus) | 10-30 | Dorsum | 22-23 | 1-3 | Hind limb, caudal thigh | 22-23 | 25-50 | Peritoneum | 20 | 5-10 | Saphenous vein | 22-23 | - | - | - | ||||
| Squirrel monkey | 5-10 | Scuff | 20 | 1-3 | Quadriceps, posterior thigh, triceps | 20 | 25-50 | Peritoneum | 20 | 0.5-1 | Femoral vein | 21 | - | - | - | ||||
*Data from guidelines for injection methods[13]
Table 3: Guidelines for maximum injection volume, by species, site location, and gauge size*
Suppose the concentration of the formulation (say nanoparticles) is 10 mg/mL, its AED is 62 mg/kg, the rat weight is 250 g and is administered through intraperitoneal route, and then the injection volume is calculated as
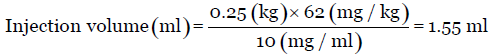
The injection volume observed here (1.55 mL) is well below the maximum injection volume (5–10 mL) for rat through intraperitoneal route and the injection site is lower left quadrant [Table 3].
Conclusion
Dose estimation always requires careful consideration about the difference in pharmacokinetics and pharmacodynamics among species. Allometric scaling assists scientists to exchange doses between species during research, experiments, and clinical trials. Different equations described in this review could be used for dose extrapolation among species. Allometric scaling is generally used to convert doses among the species and is not preferred within species.
Acknowledgment
Authors are grateful to Dr. Mohamed A. Morsy, College of Clinical Pharmacy, King Faisal University for his perceptive discussions and expert advice during the preparation of manuscript.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
References
- Reigner BG, Blesch KS. Estimating the starting dose for entry into humans: Principles and practice. Eur J Clin Pharmacol 2002;57:835-45.
- Contrera JF, Matthews EJ, Kruhlak NL, Benz RD. Estimating the safe starting dose in phase I clinical trials and no observed effect level based on QSAR modeling of the human maximum recommended daily dose. Regul Toxicol Pharmacol 2004;40:185-206.
- Lavé T, Luttringer O, Poulin P, Parrott N. Interspecies scaling. In: Krishna R, editor. Applications of Pharmacokinetic Principles in Drug Development. New York: Springer Science and Business Media, LLC; 2004. p. 133-75.
- Sharma V, McNeill JH. To scale or not to scale: The principles of dose extrapolation. Br J Pharmacol 2009;157:907-21.
- Chaturvedi PR, Decker CJ, Odinecs A. Prediction of pharmacokinetic properties using experimental approaches during early drug discovery. Curr Opin Chem Biol 2001;5:452-63.
- Rhomberg LR, Lewandowski TA. Methods for identifying a default cross-species scaling factor. Hum Ecol Risk Assess 2006;12:1094-127.
- USFDA. Guidance for Industry: Estimating the Maximum Safe Starting Dose in Adult Healthy Volunteer. Rockville, MD: US Food and Drug Administration; 2005.
- Banavar JR, Moses ME, Brown JH, Damuth J, Rinaldo A, Sibly RM, et al. A general basis for quarter-power scaling in animals. Proc Natl Acad Sci U S A 2010;107:15816-20.
- White CR, Kearney MR. Metabolic scaling in animals: Methods, empirical results, and theoretical explanations. Compr Physiol 2014;4:231-56.
- Lowe PJ, Tannenbaum S, Wu K, Lloyd P, Sims J. On setting the first dose in man: Quantitating biotherapeutic drug-target binding through pharmacokinetic and pharmacodynamic models. Basic Clin Pharmacol Toxicol 2010;106:195-209.
- Shin JW, Seol IC. Interpretation of animal dose and human equivalent dose for drug development. J Korean Orient Med 2010;31:1-7.
- Zou P, Yu Y, Zheng N, Yang Y, Paholak HJ, Yu LX, et al. Applications of human pharmacokinetic prediction in first-in-human dose estimation. AAPS J 2012;14:262-81.
- Animal Care and Use Program, Duke University and Medical Center. Available from: http://www.vetmed.duhs.duke.edu/GuidelinesforInjectionMethods.html. [Last accessed on 2015 Oct 01].